Monochromator principles of operation

Although many detailed variations are possible, most monochromators are of the same basic design, which is generally known as the Czerny-Turner configuration, and ours is no exception. Its operation is quite easy to understand, but this topic is not well covered by standard optical texts, and we therefore give a basic description here. 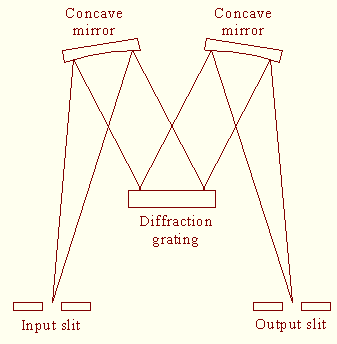This description will also explain the particular features of our own design, and will also explain the very important interaction between bandwidth and optical throughput, which our real-time slit width control system can fully exploit. The standard Czerny-Turner configuration is shown below. Light from an appropriate source (a xenon arc in our case) is focussed onto an input slit, and light passing through this slit is collimated by a concave mirror, which also reflects it onto a diffraction grating. The grating in turn directs the light onto a second concave mirror, which reflects and focusses it onto an exit slit before it leaves the instrument. Mirrors are used rather than lenses because they do not introduce any chromatic aberration, but they do introduce other aberrations which limit the resolution of the instrument, as will be discussed shortly. Since the redirection of the light beam by the grating is actually a diffraction rather than an ordinary reflection, the grating disperses the beam, i.e. different wavelengths leave the grating at different angles. By rotating the grating about its central axis, we can vary the range of wavelengths which can be reflected and focussed by the second mirror onto the exit slit.

Standard Czerny-Turner configuration

The figure below shows how a reflective grating works. This is a horizontal section through the grating, which resembles a saw blade. Viewed face on, the "teeth" are actually grooves, and the two slits in the instrument are parallel with them. (Slits can be used rather than circular apertures because the grating disperses light only in the horizontal direction, so by lengthening the apertures in the vertical direction we can get more light through the instrument without losing any resolution). Imagine a light beam arriving at a direction perpendicular to the grating. If the grating just acted as a mirror, the beam would be reflected straight back again, and indeed, some proportion of the light is reflected in this way, but in this case it is referred to as the zero-order diffracted beam. However, the grooves are shaped so that most of the light leaves the grating at a different angle, corresponding to the first-order diffracted beam. This angle corresponds to the one where reflections f rom adjacent teeth give optical patch length differences of exactly one wavelength. Since the angle is therefore wavelength-dependent, the diffracted beam actually forms a spectrum, from which we can select the required wavelengths by focussing them onto the exit slit.

Principle of operation of reflection grating

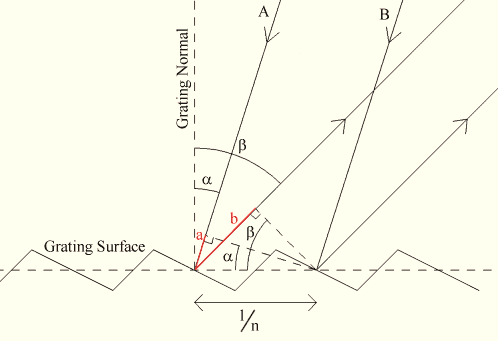
In the Czerny-Turner configuration, this is done by rotating the grating so that the required wavelength is always reflected at the same angle. This means that the angle of the incoming light also changes, but that doesn't have any major impact apart from making the calculations somewhat more interesting. The angles of the incoming and outgoing beams are conventionally referred to as a and b respectively, and although they both change when the grating is rotated, the difference between them, conventionally referred to as D, remains constant. Note that a and b are both measured with respect to the grating normal, and they will be of opposite signs if they are on opposite sides of the grating normal.

The basic grating equation is given by:

where l is the wavelength in nm, k is the diffraction order and n is the number of lines per mm for the grating. This can be rearranged in terms of the wavelength to give:

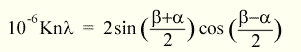
For a given instrument the deviation D is fixed and given by:

so we can express b in terms of D and a and then solve for a to obtain:

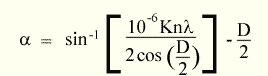
For reference, n for our standard grating is 1200 lines/mm, k is always 1 (i.e. first-order diffraction) and D in our instrument is 20 degrees. The sensitivity of the electrical input which controls the grating angle is 0.25 volts per degree. Users who wish to make their own arrangements for driving the monochromator can therefore substitute these values into equation (4) in order to calculate the appropriate drive voltage for a given wavelength. However, users who also have our microprocessor control box do not need to become involved with any of this, as the microprocessor performs these calculations itself, so the required wavelengths can be specified directly.

There are also maxima corresponding to path length differences of two or more wavelengths, giving second- and other higher-order diffracted beams (this series continues up to the maximum possible diffracted angle of 90 degrees), and there is another complete set of diffracted beams at the same angles on the other side of the incoming beam. However, by appropriately shaping the grooves in the grating, which is termed blazing, it is possible to direct most of the diffracted light into a particular ONE of these several destinations, over a reasonably wide range of wavelengths. The wavelength at which this occurs most efficiently is known as the blaze wavelength, and we use a grating with a blaze wavelength of 400nm in order to obtain highest grating efficiency (of around 70% into the required first order diffracted beam) in the near UV, for optimum results with indicators such as fura-2 and indo-1. However, the efficiency is still above 50% over most of the visible spectrum too.

Although a number of other configurations have been described, nothing else seems able to beat the performance of the Czerny-Turner, particularly in respect of the (for biological fluorescence applications) requirement for high optical throughput, which we discuss below. In our opinion the only viable alternative is one in which the grating itself is concave, so that the two concave mirrors are no longer required. However, the substantially higher cost of such gratings (which must be custom designed) makes the instrument more expensive overall. Conventional plane gratings are much cheaper, and our suppliers can provide gratings with almost any required characteristics at the same relatively low cost. The standard grating we supply has 1200 line lines/mm, blazed at 400nm, since we believe it represents the best overall compromise for this type of instrument. However, just about any other required characteristic can be supplied to special order.

Grating